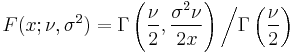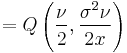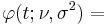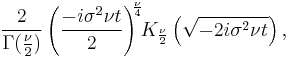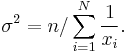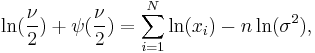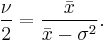Scaled-inverse-chi-squared distribution
| Probability density function None uploaded yet |
|
| Cumulative distribution function None uploaded yet |
|
| Parameters |   |
|---|---|
| Support | 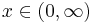 |
![\frac{(\sigma^2\nu/2)^{\nu/2}}{\Gamma(\nu/2)}~
\frac{\exp\left[ \frac{-\nu \sigma^2}{2 x}\right]}{x^{1%2B\nu/2}}](/2012-wikipedia_en_all_nopic_01_2012/I/7b7c9f0a416982abe93780545814069a.png) |
|
| CDF | 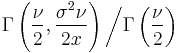 |
| Mean | 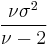 for for 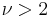 |
| Mode | 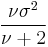 |
| Variance | 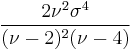 for for 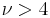 |
| Skewness | 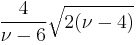 for for 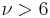 |
| Ex. kurtosis | 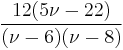 for for 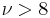 |
| Entropy | 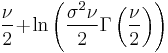
|
| MGF | 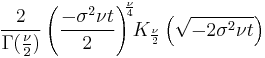 |
| CF | 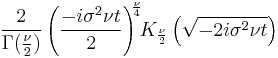 |
The scaled inverse chi-squared distribution arises in Bayesian statistics. The family of scaled inverse chi-squared distributions contains an extra scaling parameter compared to the inverse-chi-squared distribution, and it is essentially the same family of distributions as the inverse gamma distribution, but using a parametrization that may be more convenient for Bayesian statistics. Specifically, the scaled inverse chi-squared distribution can be used as a conjugate prior for the variance parameter of a normal distribution; however, it is more common to use the inverse gamma distribution formulation instead. This distribution is the maximum entropy distribution for a fixed first inverse moment 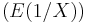 and first logarithmic moment
and first logarithmic moment 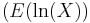 .
.
Characterization
The probability density function of the scaled inverse chi-squared distribution extends over the domain 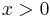 and is
and is
where  is the degrees of freedom parameter and
is the degrees of freedom parameter and 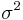 is the scale parameter. The cumulative distribution function is
is the scale parameter. The cumulative distribution function is
where 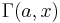 is the incomplete Gamma function,
is the incomplete Gamma function, 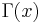 is the Gamma function and
is the Gamma function and 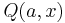 is a regularized Gamma function. The characteristic function is
is a regularized Gamma function. The characteristic function is
where 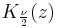 is the modified Bessel function of the second kind.
is the modified Bessel function of the second kind.
Parameter estimation
The maximum likelihood estimate of 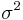 is
is
The maximum likelihood estimate of  can be found using Newton's method on:
can be found using Newton's method on:
where 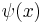 is the digamma function. An initial estimate can be found by taking the formula for mean and solving it for
is the digamma function. An initial estimate can be found by taking the formula for mean and solving it for 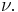 Let
Let 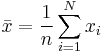 be the sample mean. Then an initial estimate for
be the sample mean. Then an initial estimate for  is given by:
is given by:
Related distributions
- If
 then
then 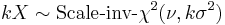
- If
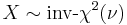 (Inverse-chi-squared distribution) then
(Inverse-chi-squared distribution) then 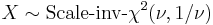
- If
 then
then 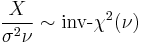 (Inverse-chi-squared distribution)
(Inverse-chi-squared distribution) - If
 then
then 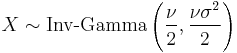 (Inverse-gamma distribution)
(Inverse-gamma distribution) - Scaled inverse chi square distribution is a special case of type 5 Pearson distribution

![f(x; \nu, \sigma^2)=
\frac{(\sigma^2\nu/2)^{\nu/2}}{\Gamma(\nu/2)}~
\frac{\exp\left[ \frac{-\nu \sigma^2}{2 x}\right]}{x^{1%2B\nu/2}}](/2012-wikipedia_en_all_nopic_01_2012/I/83990c30519192fce1b53a864db50ad8.png)